TPE sur le son 2007-2008

Calcul du rapport entre les fréquences d'un demi-ton

Tempérer une gamme revient donc à modifier légèrement la fréquence des notes afin d'avoir un rapport constant entre demi-tons. Ainsi les rapports de fréquences suivants doivent être tous égaux :

Chacun de ces rapports est égal à une constante a, que l'on calcule en effectuant la multiplication de ces 12 rapports. On obtient ainsi :
La valeur de la constante a est la racine 12ème de 2, afin de conserver un rapport idéal de fréquences de 2 pour une octave. L’homme qui a trouvé ce rapport n’est autre que Jean Sébastien Bach.

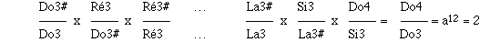
a = 1, 059 463

Le La est la seule note à conserver sa fréquence dans ce nouveau système, ainsi La3 = 440 Hz dans les deux gammes. Cette fréquence va servir de base de calcul pour toutes les autres notes.

Fréquence du Si3 : Si3/La3# x La3#/La3 = Si3/La3 = a2
Deux notes séparées d'un ton auront ainsi un rapport de fréquences de a2.
Si3 = a2 x La3 = (1,0595)2 x 440 = 493,9 Hz

Fréquence du Do4 : Do4/Si3 x Si3/La3 = Do4/La3 = a3
Deux notes séparées de 3 demi-tons auront ainsi un rapport de fréquences de a3.
Do4 = a3 x La3 = (1,0595)3 x 440 = 523,3 Hz

Pour les fréquences des autres notes, il suffit de remarquer que deux notes séparées de n demi-tons ont un rapport de fréquences de a^n.

Fréquence du Ré4 : Ré4/La3 = a5 (5 demi-tons)
Ré4 = a5 x La3 = (1,0595)5 x 440 = 587,3 Hz

Fréquence du Mi4 : Mi4/La3 = a7 (7 demi-tons)
Mi4 = a7 x La3 = (1,0595)7 x 440 = 659,3 Hz

Fréquence du Fa4 : Fa4/La3 = a8 (8 demi-tons)
Fa4 = a8 x La3 = (1,0595)8 x 440 = 698,5 Hz

Fréquence du Sol4 : Sol4/La3 = a10 (10 demi-tons)
Sol4 = a10 x La3 = (1,0595)10 x 440 = 784,0 Hz

Les fréquences des autres notes se calculent, soit en utilisant la relation entre le nombre de demi-tons et l'exposant n, soit le rapport entre deux notes formant une octave.

Do2	130,8
Re2	146,8
Mi2	164,8
Fa2	174,6
Sol2	196,0
La2	220,0
Si2	246,9
Do3	261,6
Re3	293,7
Mi3	329,6
Fa3	349,2
Sol3	392,0
La3	440,0
Si3	493,9
Do4	523,3
Re4	587,3
Mi4	659,3
Fa4	698,5
Sol4	784,0
La4	880,0
Si4	987,8

Harmonie

L’harmonie est, dans son sens le plus large désignée comme la troisième composante de la musique, les deux premières étant respectivement, le rythme et la mélodie, la quatrième étant le timbre. —. L'harmonie relève de l'utilisation délibérée de fréquences simultanées, dans la perspective d'apporter relief et profondeur au chant ou au jeu instrumental : elle représente donc l'aspect vertical de la musique, tandis que la mélodie en représente l'aspect horizontal.
Par exemple pour la note Do2 on constate l’apparition deux autres notes qui sont Sol3 et Do3 et Mi4, d’autres notes viendront s’ajouter au spectre harmonique mais elles sont de plus en plus faible intensité comme le montre ce graphique.
Le Do2 est appelé la fondamentale sa fréquence est 130.8
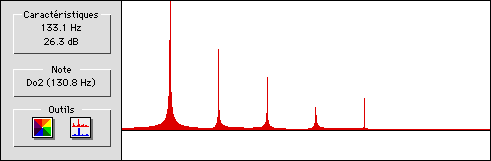
Le Sol3 est appelé la dominante (quinte de do) sa fréquence est 392
Le Do3 est l’octave du Do2 sa fréquence est 261.8
Le Mi4 est la médiante (tierce de do) sa fréquence est 669.3

Le son peut donc être gradué, grâce à cette science appelée le solfège qui est très proche des mathématiques. Il existe de multiples relations entre les sons, et si le résonnement est faux le résultat sera faux et la mélodie sera fausse. Le solfège est donc en quelque sorte l’illustration mélodique des mathématiques.