TPE sur le son 2007-2008

L'octave est un intervalle représentant 8 notes, et comportant 12 demi-tons. Le rapport de fréquence associé à cet intervalle est 2. Comme indiqué plus haut, pour monter d'une octave il suffit de doubler la fréquence du son. Cette propriété a été démontrée par Pythagore. En effet celui-ci a tendu une ficelle et l’a grattée, il s’est ensuite aperçu que lorsqu’il coupait cette ficelle en deux parties égales, il obtenait, en tendant l’un des deux morceaux la note située à l’octave au dessus de celle qu’il avait obtenue auparavant.

La quinte est un intervalle représentant 5 notes, et comportant 7 demi-tons, comme l'intervalle Do3-Sol3. Le rapport idéal de fréquence associé à cet intervalle est 3/2. En effet, la fréquence du Do3 étant le double de celle du Do2, et la fréquence du Sol3 étant le triple de celle du Do2, la fréquence du Sol3 est donc égale à celle du Do3 multipliée par 3/2.

Ces deux théories peuvent être démontrées par l’expérience suivante :

Le principe est simple, il s’agit, pour commencer, de faire vibrer une corde à fréquence constante donnée α:

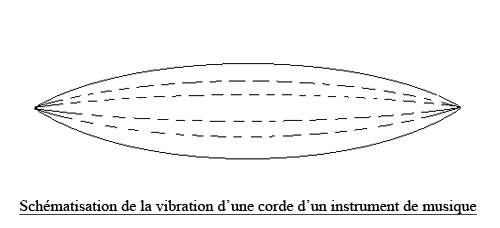
La corde va osciller du haut vers le bas, elle va créer une onde.
Nous allons ensuite placer ce que nous allons appeler des nœuds de vibration à intervalles réguliers qui seront des points immobiles placés sur la corde et qui ne vibreront pas.

On constate que postérieurement à la pose des nœuds, la fréquence d’oscillation entre deux nœuds est égale à la fréquence initiale multipliée par le nombre de ventres crées.
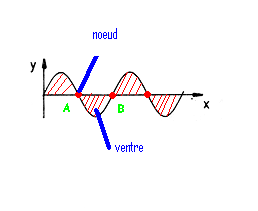
Pour notre exemple : la fréquence d’oscillation entre A et B est égale à : α multiplié par 4.

Grâce à cette expérience, dans laquelle l’onde sonore est matérialisée par une corde, nous pouvons mieux comprendre le rapport entre un intervalle donné et la fréquence de l’onde.

Sachant que la fréquence du La3 est 440 Hertz on peut remplir le tableau suivant :

Do2	132
Re2	148,5
Mi2	165
Fa2	176
Sol2	198
La2	220
Si2	247,5
Do3	264
Re3	297
Mi3	330
Fa3	352
Sol3	396
La3	440
Si3	495
Do4	528
Re4	594
Mi4	660
Fa4	704
Sol4	792
La4	880

Défaut de la gamme naturelle

Avec les notes de la gamme en Do, on ne peut construire que 6 quintes, l'intervalle Si3 - Fa4 ne comportant que 6 demi-tons au lieu de 7 pour une quinte. Les notes formant ces intervalles doivent avoir des fréquences ayant un rapport idéal de 3/2.

Quinte Do3 - Sol3 : Sol3/Do3 = 396/264 = 1,5 = 3/2
Quinte Fa3 - Do4 : Do4/Fa3 = 528/352 = 1,5 = 3/2
Quinte Sol3 - Ré4 : Ré4/Sol3 = 594/396 = 1,5 = 3/2
Quinte Mi3 - Si3 : Si3/Mi3 = 495/330 = 1,5 = 3/2
Quinte La3 - Mi4 : Mi4/La3 = 660/440 = 1,5 = 3/2

Ces résultats ne sont pas surprenants, car ils résultent de la construction de la gamme. Si les 5 premières quintes ont bien un rapport idéal de fréquences, la dernière est légèrement dissonante, comme le montre le calcul ci-dessous.

Quinte Ré3 - La3 : La3/Ré3 = 440/297 = 1,48 3/2

La solution à ce problème est de tempérer la gamme, afin que le rapport de fréquences entre demi-tons soit constant. On construit ainsi une gamme appelée gamme chromatique car elle est constituée de 12 demi-tons.